Investigation

Was there a better time to be a hi-fi enthusiast than the late 1970s and early 1980s? It's hard to argue against it because there was so much going on, what with the development of digital audio on one hand and the rise of subjectivism on the other. Suddenly turntables and amplifiers were no longer judged by wow and flutter, rumble and price tag or power output, total harmonic distortion and price tag, but by listening to them. Shock, horror! And it was possible to talk about the sound of cables without being carted off in a straitjacket. In this new atmosphere, everything once taken for granted in hi-fi became a candidate for reassessment.

One area that came in for close scrutiny was the sonic effect of passive components in electronics: resistors, inductors and capacitors – especially capacitors. Those in the know began to talk about equivalent series resistance and dielectric absorption; electrolytic capacitors were out, film capacitors were in.

It's a subject we don't hear so much about now but not because the issue has gone away. Rather, most audiophile circuit designers now pay as close attention to the passive components they use as to the circuits they put them into. So the public furore has died down.

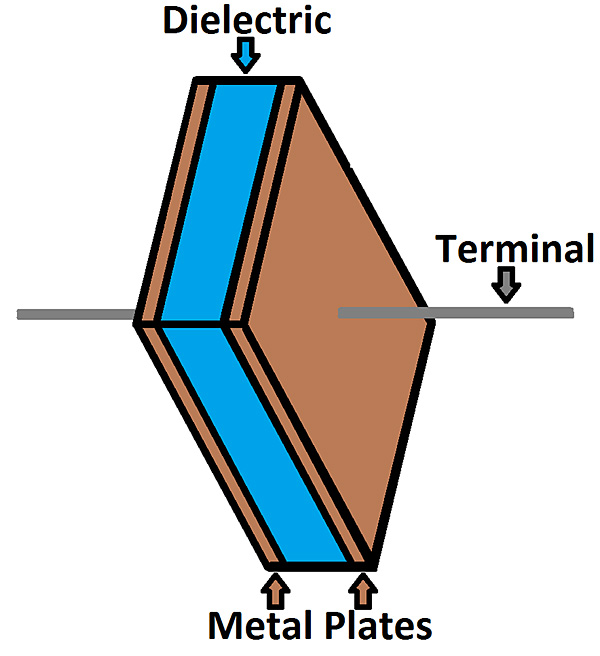
In its simplest form a capacitor comprises two metal plates separated by air (or even better a vacuum) – see Fig 1. Because there is no conductive path between the plates, the capacitor blocks the flow of direct current (eg, from a battery). Indeed, this is one of the classic job descriptions for a capacitor, allowing one part of a circuit to operate at a DC voltage that is different from other parts, or from the outside world – something that's possible because a capacitor does, by contrast, pass non-constant, fluctuating, AC signals such as a music waveform.

Solid Solutions
You don't often encounter air capacitors, although if you've ever peered inside an old AM radio and seen a tuning element comprising interleaved, spaced metal plates, that is an air capacitor: a variable one. Most of the capacitors we encounter in audio and other electronics don't use air as the insulating material (aka dielectric) that separates the plates because air has a low dielectric constant (1.0), which means that air capacitors of large capacitance are too bulky to be practical. So other, mostly solid dielectrics, with higher dielectric constants, are used, including materials such as ceramics and various types of plastic (eg, PVC which has a dielectric constant of 4.0). Which is where the story gets interesting since these dielectrics all have performance trade-offs, whereas air is pretty much perfect.

Simple Filters
That's a tale that must wait a moment, though, because first we need to know more about how capacitors behave and what they are used for. Capacitors block DC and pass AC, but they don't pass AC of different frequencies with equal facility. Capacitors have reactance, and that reactance decreases as frequency increases. (Inductors have reactance too but it behaves the opposite way, increasing with increasing frequency.)

So capacitors pass higher frequency signals more readily than lower frequency signals, a property which makes them valuable in frequency-selective circuits, ie, filters, and in supply decoupling applications where a capacitor connected to ground provides a low impedance path to remove unwanted AC signals (eg, hum, noise) from a DC supply rail.

Simple resistance-capacitance high-pass and low-pass filters are shown in Fig 2. In the high-pass filter (Fig 2a) a series capacitor is connected to a shunt resistor. At very low frequencies, the reactance of the capacitor is much higher than the resistance of the resistor, so little signal voltage appears across the resistor. Whereas at very high frequencies, the capacitor's reactance is small compared to the resistor's resistance and so the signal is passed with little attenuation.

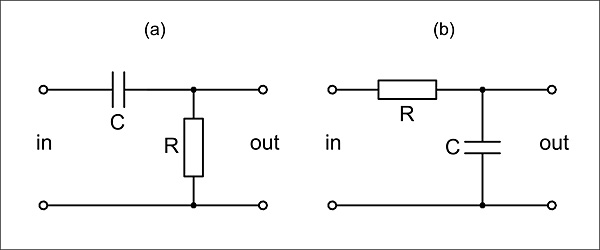
In the low-pass filter (Fig 2b), the positions of the capacitor and resistor are swapped. Now the high reactance of the capacitor at very low frequencies ensures that the signal is barely attenuated, whereas at very high frequencies its low reactance means that signal attenuation is high.

On A Roll
These simple RC filter circuits are termed first-order filters and have ultimate roll-offs of 6dB per octave. In other words, signal voltage decreases by half for each halving (high-pass) or doubling (low-pass) of signal frequency. Their frequency responses are shown in Fig 3, where the centre value 1 on the frequency scale – where the attenuation is 3dB – is called the corner frequency (or cut-off frequency or break frequency) and corresponds to 1/(2πRC), where R is the resistor's resistance in ohms and C is the capacitor's capacitance in farads.

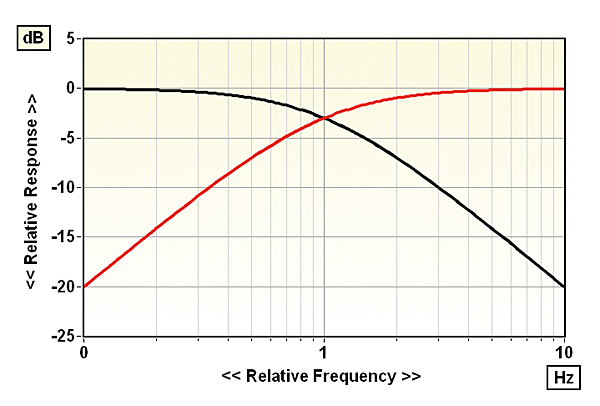
If we choose example values of 10,000ohm (10kohm) and 1μF (one microfarad), the corner frequency will be at just under 16Hz. Higher-order filters, requiring more components, have ultimate roll-off rates which are multiples of 6dB per octave, ie, 12dB/octave for a second-order filter, 18dB/octave for a third-order filter, etc.

We've seen thus far that capacitors are used for coupling circuits together, for decoupling noise from DC voltage rails, and within frequency-selective circuits (filters). Because capacitors store electric charge, large ones are also used as reservoirs in AC to DC power supplies. Fig 4 shows a basic full-wave rectified power supply comprising a step-down transformer (which reduces the mains voltage), a full-wave bridge rectifier (which converts the stepped-down AC from the transformer into pulsed DC) and twin reservoir capacitors (which prop up the voltage when the rectifier isn't conducting, thereby smoothing the pulsed DC so that it's close to a steady DC voltage).

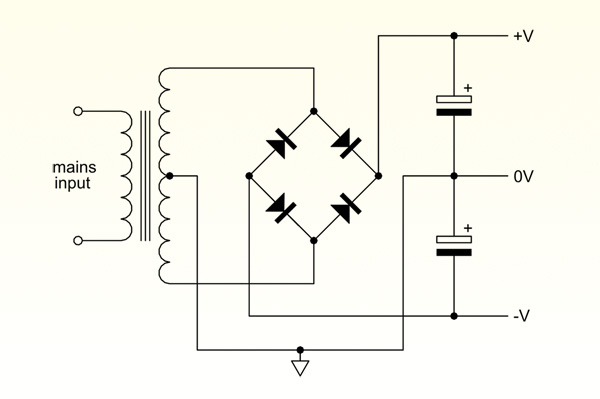
Circuits of this type are found in many solid-state electronic audio components and similar circuits are used in valve equipment although, due to the high operating voltages required by valves, the transformer normally steps up the mains voltage, and there is typically a single supply rail rather than dual rails.

A reservoir capacitor behaves like a decoupling capacitor in that it bleeds off unwanted AC to earth, but it does so on a grand scale. The reservoir capacitance used in solid-state power amplifiers can be 50,000µF (0.05F) or more per rail, whereas elsewhere the circuit may use capacitors of 1nF (one-thousandth of a microfarad) or less. So the range of capacitance required in electronic circuits can be huge: nine orders of magnitude or thereabouts. Unsurprisingly, this means that different capacitor types are better adapted to certain roles than are others.

Practical Note
Reservoir capacitors, the largest, are usually aluminium electrolytic types because these provide high capacitance in a practicably small volume. Because electrolytic capacitors incorporate an electrolyte (a liquid or gel containing ions) which reacts chemically with the metal foil within the can to form the dielectric layer, they have to be connected the right way round so that the positive terminal is operated at a higher DC voltage than the negative terminal. Such capacitors – and there are other examples, notably tantalum capacitors – are termed polar, and not observing their polarity can result in their catastrophic failure.